- For lukket krets
- Separat seksjon og komplett elektrisk krets
- Beregning av den nåværende delen av den elektriske kretsen
- Beregningsmulighet for en komplett kjede
- Lovens effekt på en variabel
- EMF-kilde i en komplett krets
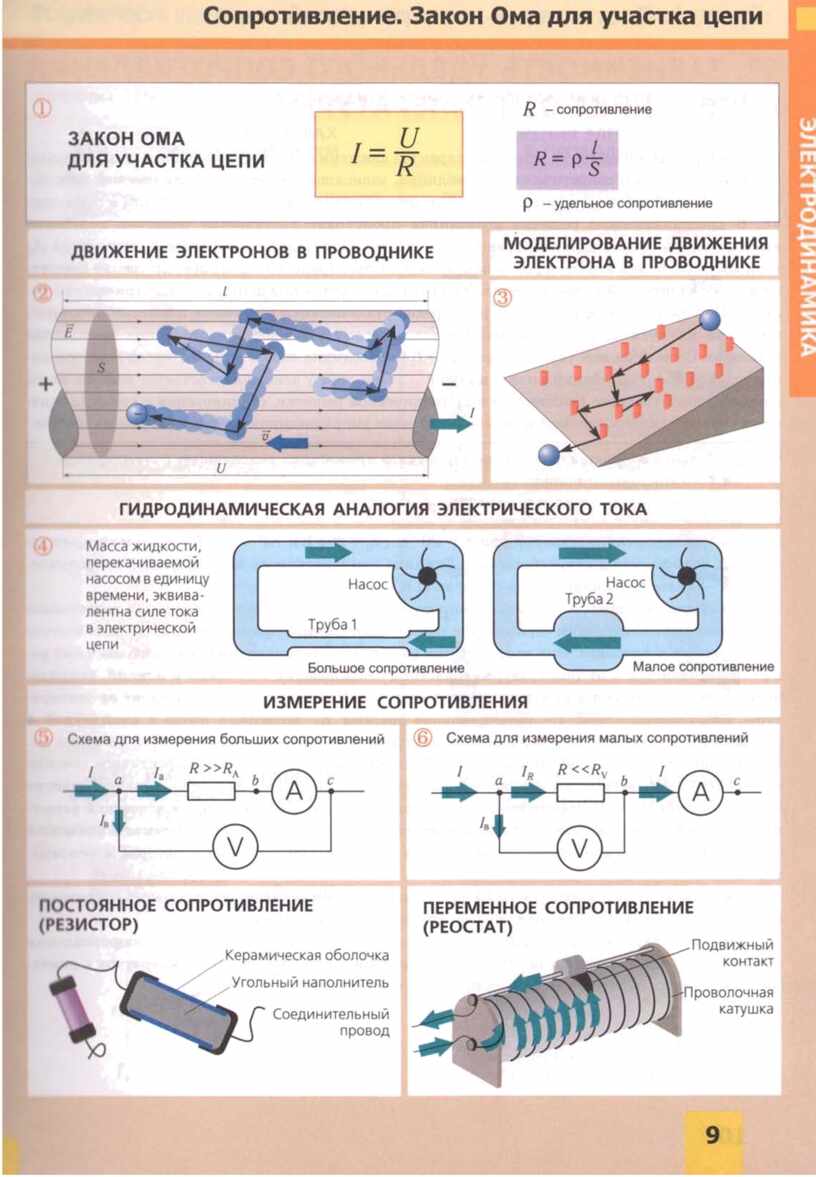
- R - elektrisk motstand
- Ujevn del av DC-kretsen
- Seriell og parallell kobling av elementer
- En kjede av seriekoblede resistive elementer
- En kjede av parallellkoblede resistive elementer
- Integrerte og differensielle former for loven
- Forstå strøm og motstand
- Ohms lov for vekselstrøm
- Når Ohms lov inntreffer
- Kirchhoffs lover.
- Enkle konsepter
- Styrke og spenning
- Ledermotstand
- Ohms lovtolkning
- Parallell og seriell tilkobling
- seriell tilkobling
- Parallellkobling
- Hva gir oss en parallell og seriell forbindelse?
- Ideell EMF-kilde
- I differensiell form
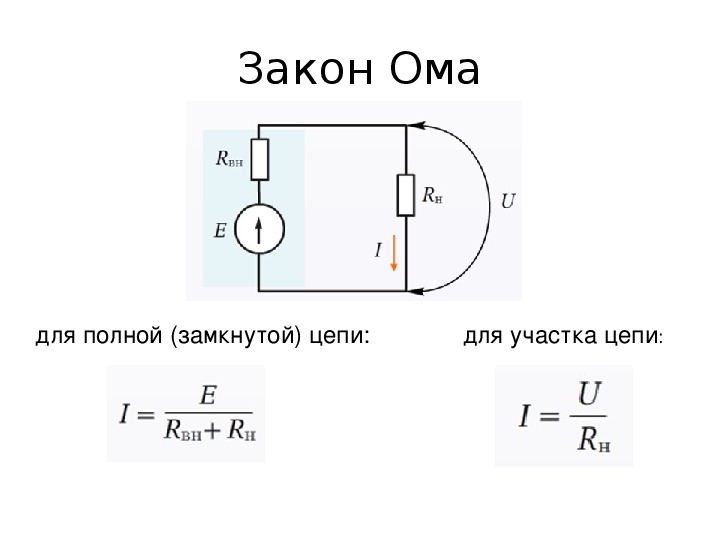
For lukket krets
En lukket krets betyr en lukket elektrisk forbindelse som strøm sirkulerer gjennom. Når det er en serie ledninger som kobles til hverandre og fullfører kretsen slik at jeg går fra den ene enden av sirkelen til den andre, vil det være en lukket krets.
EMF (E) - betegnet og målt i volt og refererer til spenningen generert av et batteri eller magnetisk kraft i henhold til Faradays lov, som sier at et tidsvarierende magnetfelt vil indusere en elektrisk strøm.
Da: E = IR + Ir
E \u003d I (R + r)
I \u003d E / (R + r)
Hvor: r er motstanden til strømkilden.
Dette uttrykket er kjent som Ohms lov om lukkede kretser.
Heterogen kjede
Separat seksjon og komplett elektrisk krets
Ohms lov, brukt på en seksjon eller hele kretsen, kan vurderes i to beregningsalternativer:
- Egen kort seksjon. Det er en del av en krets uten en EMF-kilde.
- En komplett kjede bestående av en eller flere seksjoner. Dette inkluderer også en EMF-kilde med egen indre motstand.
Beregning av den nåværende delen av den elektriske kretsen
I dette tilfellet brukes den grunnleggende formelen I \u003d U / R, der I er strømstyrken, U er spenningen, R er motstanden. I følge den kan man formulere den allment aksepterte tolkningen av Ohms lov:
Denne formuleringen er grunnlaget for mange andre formler presentert på den såkalte "kamillen" i grafisk design. I sektor P - bestemmes kraft, i sektor I, U og R - utføres handlinger relatert til strømstyrke, spenning og motstand.
Hvert uttrykk - både grunnleggende og tillegg, lar deg beregne de nøyaktige parametrene til elementene beregnet for bruk i kretsen.
Spesialister som jobber med elektriske kretser utfører en rask bestemmelse av noen av parameterne ved å bruke trekantmetoden vist i figuren.
Beregningene bør ta hensyn til motstanden til lederne som forbinder elementene i seksjonen. Siden de er laget av forskjellige materialer, vil denne parameteren være forskjellig i hvert enkelt tilfelle.Hvis det er nødvendig å danne en komplett krets, er hovedformelen supplert med parametrene til en spenningskilde, for eksempel et batteri.
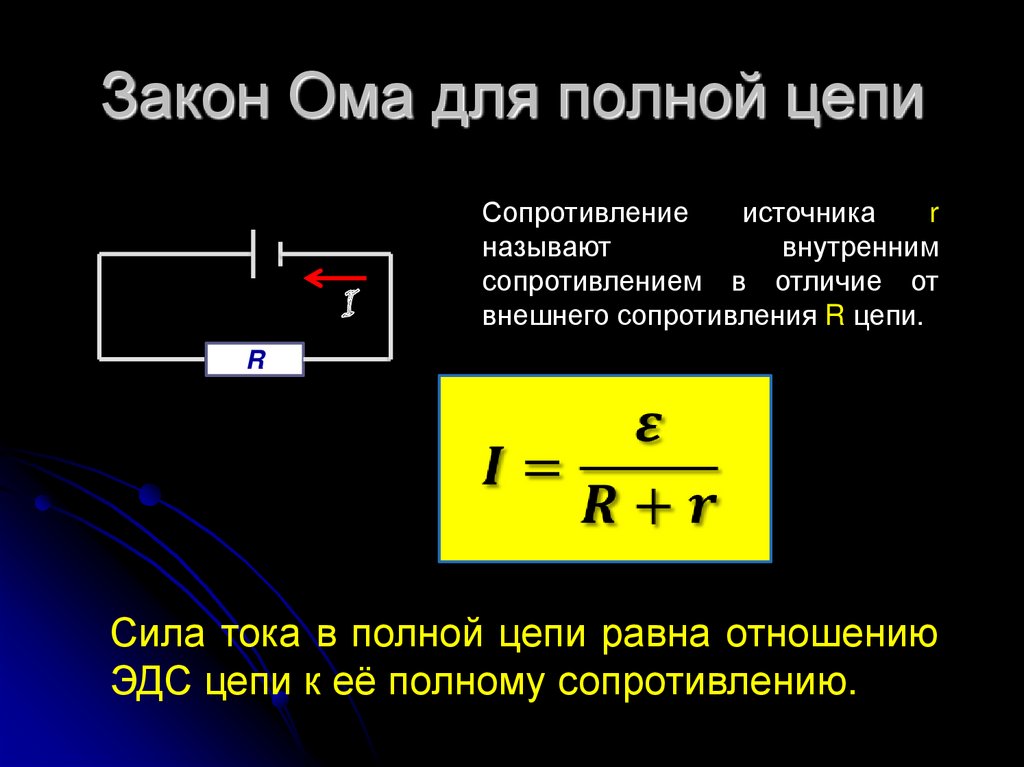
Beregningsmulighet for en komplett kjede
En komplett krets består av individuelle seksjoner, kombinert til en enkelt helhet sammen med en spenningskilde (EMF). Dermed blir den eksisterende motstanden til seksjonene supplert med den interne motstanden til den tilkoblede kilden. Derfor vil hovedtolkningen diskutert tidligere lyde som følger: I = U / (R + r). Den resistive eksponenten (r) til EMF-kilden er allerede lagt til her.
Fra synspunktet til ren fysikk anses denne indikatoren som en veldig liten verdi. Men i praksis, når man beregner komplekse kretser og kretser, er spesialister tvunget til å ta det i betraktning, siden ytterligere motstand påvirker nøyaktigheten av arbeidet. I tillegg er strukturen til hver kilde veldig heterogen, som et resultat kan motstanden i noen tilfeller uttrykkes med ganske høye priser.
Ovennevnte beregninger er utført i forhold til DC-kretser. Handlinger og beregninger med vekselstrøm gjøres i henhold til et annet opplegg.
Lovens effekt på en variabel
Med vekselstrøm vil motstanden til kretsen være den såkalte impedansen, bestående av aktiv motstand og reaktiv resistiv belastning. Dette skyldes tilstedeværelsen av elementer med induktive egenskaper og en sinusformet strømverdi. Spenning er også en variabel, som fungerer i henhold til dens svitsjelover.
Derfor beregnes Ohms lov AC-kretsdesign under hensyntagen til spesifikke effekter: ledende eller etterslepende størrelsen på strømmen fra spenningen, samt tilstedeværelsen av aktiv og reaktiv effekt.I sin tur inkluderer reaktans induktive eller kapasitive komponenter.
Alle disse fenomenene vil tilsvare formelen Z \u003d U / I eller Z \u003d R + J * (XL - XC), der Z er impedansen; R - aktiv belastning; XL, XC - induktive og kapasitive belastninger; J er korreksjonsfaktoren.
EMF-kilde i en komplett krets
For forekomst av elektrisk strøm i en lukket krets, må denne kretsen inneholde minst ett spesielt element der arbeidet med å overføre ladninger mellom polene vil finne sted. Kreftene som bærer ladninger inne i dette elementet gjør det mot det elektriske feltet, noe som betyr at deres natur må være forskjellig fra elektrisk. Derfor kalles slike styrker tredjepart.
Ris. 1. Ytre krefter i fysikk.
Et element i en elektrisk krets der eksterne krefter jobber for å overføre ladninger mot virkningen av et elektrisk felt kalles en strømkilde. Dens viktigste kjennetegn er størrelsen på ytre krefter. For å karakterisere det, er et spesielt mål introdusert - Elektromotorisk kraft (EMF), det er betegnet med bokstaven $\mathscr{E}$.
Verdien av EMF til gjeldende kilde er lik forholdet mellom eksterne krefter for overføring av ladning til verdien av denne ladningen:
$$\mathscr{E}={A_{st}\over q}$$
Siden betydningen av EMF er veldig nær betydningen av elektrisk spenning (gjenkalling, spenning er forholdet mellom arbeidet utført av det elektriske feltet som bærer ladningen og verdien av denne ladningen), så måles EMF, som spenning, i Volt:
$$1B={J\overCl}$$
Den nest viktigste elektriske egenskapen til en reell strømkilde er dens indre motstand.Når ladninger overføres mellom terminalene, samhandler de med stoffet til EMF-kilden, og derfor gir kilden for elektrisk strøm også en viss motstand. Intern motstand, som vanlig motstand, måles i ohm, men er betegnet med den lille latinske bokstaven $r$.

Ris. 2. Eksempler på aktuelle kilder.
R - elektrisk motstand
Motstand er det gjensidige av spenning og kan sammenlignes med effekten av å bevege en kropp mot bevegelse i rennende vann. Enheten til R er Om, som er betegnet med den store greske bokstaven Omega.
Den resiproke motstanden (1/R) er kjent som konduktivitet, som måler et objekts evne til å lede en ladning, uttrykt i Siemens-enheter.
Den geometrisk uavhengige størrelsen som brukes kalles resistivitet og er vanligvis betegnet med det greske symbolet r.
Tilleggsinformasjon. Ohms lov bidrar til å etablere tre viktige indikatorer for driften av det elektriske nettverket, noe som forenkler beregningen av kraft. Det gjelder ikke for ensidige nettverk med elementer som diode, transistor og lignende. Og det er heller ikke aktuelt for ikke-lineære elementer, hvorav tyristorer er eksempler, fordi motstandsverdien til disse elementene endres med forskjellig gitt spenning og strøm.
Ved høyere frekvenser blir distribuert atferd dominerende. Det samme skjer med svært lange kraftledninger. Selv ved en frekvens så lav som 60 Hz har en veldig lang overføringslinje, for eksempel 30 km, en distribuert natur.Hovedårsaken er at de effektive elektriske signalene som forplanter seg i kretser er elektromagnetiske bølger, ikke volt og ampere, som er infisert av en elektromagnetisk bølge. Lederne fungerer rett og slett som guider for bølgene. Så for eksempel vil en koaksialkabel vise Z = 75 ohm, selv om DC-motstanden er ubetydelig.
Ohms lov er den grunnleggende loven for elektroteknikk. Den har et stort antall praktiske bruksområder i alle elektriske kretser og elektroniske komponenter.
De vanligste eksemplene på anvendelsen av Ohms lov:
- Strømmen som tilføres den elektriske varmeren. Gitt motstanden til varmespolen og den påførte spenningen, kan effekten som tilføres den varmeren beregnes.
- Valg av sikringer. De er beskyttelseskomponenter som er koblet i serie med elektroniske enheter. Sikringer/CB-er er vurdert i ampere. Gjeldende sikringsklassifisering beregnes ved å bruke Ohms lov.
- Design av elektroniske enheter. Elektroniske enheter som bærbare datamaskiner og mobiltelefoner krever en DC-strømforsyning med en bestemt strømverdi. Typiske mobiltelefonbatterier krever 0,7-1 A. En motstand brukes til å kontrollere strømmen som flyter gjennom disse komponentene. Ohms lov brukes til å beregne merkestrømmen i en typisk krets.
På en gang ble Ohms konklusjoner en katalysator for ny forskning innen elektrisitet, og i dag har de ikke mistet sin betydning, siden moderne elektroteknikk er basert på dem. I 1841 ble Om tildelt Royal Societys høyeste ære, Copley-medaljen, og begrepet "Om" ble anerkjent som en motstandsenhet allerede i 1872.
Ujevn del av DC-kretsen
En heterogen struktur har en slik del av kretsen, hvor det i tillegg til ledere og elementer er en strømkilde. Dens EMF må tas i betraktning ved beregning av den totale strømstyrken i dette området.
Det er en formel som definerer hovedparametrene og prosessene til et heterogent sted: q = q0 x n x V. Dens indikatorer er karakterisert som følger:
- I ferd med å flytte ladninger (q) får de en viss tetthet. Ytelsen avhenger av strømstyrken og tverrsnittsarealet til lederen (S).
- Under forhold med en viss konsentrasjon (n), er det mulig å nøyaktig indikere antall enhetsladninger (q0) som ble flyttet i løpet av en enkelt tidsperiode.
- For beregninger anses lederen betinget som en sylindrisk seksjon med noe volum (V).
Når du kobler lederen til batteriet, vil sistnevnte bli utladet etter en stund. Det vil si at bevegelsen av elektroner gradvis bremses ned og til slutt stopper helt. Dette forenkles av lederens molekylære gitter, som motvirker kollisjon av elektroner med hverandre og andre faktorer. For å overvinne slik motstand, må visse tredjepartskrefter brukes i tillegg.
Under beregninger blir disse kreftene lagt til Coulomb-ene. I tillegg, for å overføre en enhetsladning q fra 1. punkt til 2., vil det være nødvendig å utføre arbeidet A1-2 eller ganske enkelt A12. For dette formålet opprettes en potensiell forskjell (ϕ1 - ϕ2). Under påvirkning av en likestrømkilde oppstår en EMF som flytter ladninger langs kretsen. Størrelsen på den totale spenningen vil bestå av alle kreftene nevnt ovenfor.
Polariteten til tilkoblingen til DC-forsyningen må tas med i beregningene. Når terminalene endres, vil EMF også endre seg, akselerere eller bremse bevegelsen av ladninger.
Seriell og parallell kobling av elementer
For elementer i en elektrisk krets (seksjon av en krets) er et karakteristisk moment en serie- eller parallellforbindelse.
Følgelig er hver type tilkobling ledsaget av en annen karakter av strømstrømmen og spenningsforsyningen. På denne kontoen brukes også Ohms lov på forskjellige måter, avhengig av muligheten for å inkludere elementer.
En kjede av seriekoblede resistive elementer
Når det gjelder en seriekobling (del av en krets med to komponenter), brukes ordlyden:
- jeg = jeg1 = jeg2 ;
- U = U1 + U2 ;
- R=R1 + R2
Denne formuleringen viser tydelig at uavhengig av antall resistive komponenter koblet i serie, endrer ikke strømmen som flyter i en del av kretsen verdi.
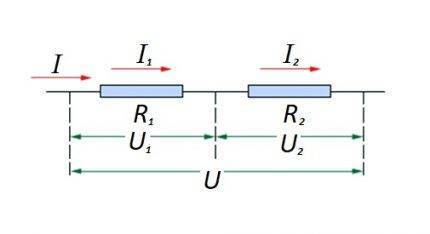 Koble resistive elementer i en kretsseksjon i serie med hverandre. Dette alternativet har sin egen beregningslov. I diagrammet: I, I1, I2 - strømflyt; R1, R2 - resistive elementer; U, U1, U2 - påført spenning
Koble resistive elementer i en kretsseksjon i serie med hverandre. Dette alternativet har sin egen beregningslov. I diagrammet: I, I1, I2 - strømflyt; R1, R2 - resistive elementer; U, U1, U2 - påført spenning
Mengden spenning som påføres de aktive resistive komponentene i kretsen er summen og summeres til verdien av EMF-kilden.
I dette tilfellet er spenningen på hver enkelt komponent: Ux = I * Rx.
Den totale motstanden bør betraktes som summen av verdiene til alle resistive komponenter i kretsen.
En kjede av parallellkoblede resistive elementer
I tilfellet når det er en parallell forbindelse av resistive komponenter, anses formuleringen som rettferdig med hensyn til loven til den tyske fysikeren Ohm:
- jeg = jeg1 + jeg2 … ;
- U = U1 = U2 … ;
- 1/R = 1/R1 + 1 / R2 + …
Alternativer for kompilering av kretsseksjoner av "blandet" type er ikke utelukket når parallelle og serielle tilkoblinger brukes.
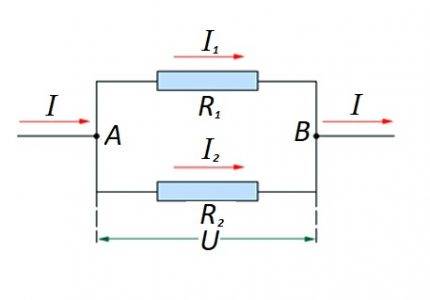 Sammenkobling av resistive elementer i en kretsseksjon parallelt med hverandre. For dette alternativet anvendes egen beregningslov. I diagrammet: I, I1, I2 - strømflyt; R1, R2 - resistive elementer; U - påført spenning; A, B - inn-/utgangspunkter
Sammenkobling av resistive elementer i en kretsseksjon parallelt med hverandre. For dette alternativet anvendes egen beregningslov. I diagrammet: I, I1, I2 - strømflyt; R1, R2 - resistive elementer; U - påført spenning; A, B - inn-/utgangspunkter
For slike alternativer utføres beregningen vanligvis ved den første beregningen av motstandsvurderingen til parallellforbindelsen. Deretter legges verdien til motstanden koblet i serie til resultatet.
Integrerte og differensielle former for loven
Alle punktene ovenfor med beregninger gjelder forhold når ledere av en "homogen" struktur, så å si, brukes som en del av elektriske kretser.
I mellomtiden må man i praksis ofte forholde seg til konstruksjonen av en skjematisk, hvor strukturen til lederne endres i forskjellige områder. For eksempel brukes ledninger med et større tverrsnitt eller tvert imot mindre, laget på grunnlag av forskjellige materialer.
For å ta hensyn til slike forskjeller er det en variant av den såkalte "differensial-integralen Ohms lov". For en uendelig liten leder beregnes strømtetthetsnivået avhengig av intensiteten og konduktivitetsverdien.
Under differensialberegningen tas formelen: J = ό * E
For integralberegningen, henholdsvis, formuleringen: I * R = φ1 - φ2 + έ
Imidlertid er disse eksemplene ganske nærmere skolen for høyere matematikk og brukes faktisk ikke i den virkelige praksisen til en enkel elektriker.
Forstå strøm og motstand
La oss starte med begrepet elektrisk strøm.Kort fortalt er elektrisk strøm i forhold til metaller den rettet bevegelse av elektroner - negativt ladede partikler. De er vanligvis representert som små sirkler. I en rolig tilstand beveger de seg tilfeldig, og endrer hele tiden retning. Under visse forhold - utseendet til en potensiell forskjell - begynner disse partiklene en viss bevegelse i en eller annen retning. Denne bevegelsen er den elektriske strømmen.
For å gjøre det klarere kan vi sammenligne elektroner med vann som er sølt på et eller annet plan. Så lenge flyet står stille, beveger ikke vannet seg. Men så snart en skråning dukket opp (en potensiell forskjell oppsto), begynte vannet å bevege seg. Det er det samme med elektroner.
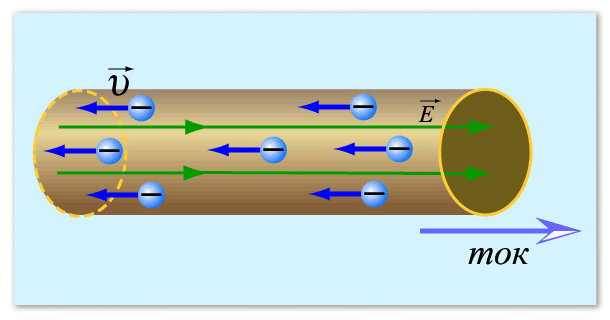
Slik kan en elektrisk strøm tenkes
Nå må vi forstå hva motstand er og hvorfor de har tilbakemelding med strømstyrke: jo høyere motstand, jo lavere strøm. Som du vet, beveger elektroner seg gjennom en leder. Vanligvis er dette metalltråder, siden metaller har god evne til å lede strøm. Vi vet at metallet har et tett krystallgitter: mange partikler som er tett og sammenkoblet. Elektroner, på vei mellom metallatomer, kolliderer med dem, noe som gjør det vanskelig for dem å bevege seg. Dette er med på å illustrere motstanden som en leder utøver. Nå blir det klart hvorfor jo høyere motstand, jo lavere strømstyrke - jo flere partikler, jo vanskeligere er det for elektroner å overvinne banen, de gjør det saktere. Dette ser ut til å ha blitt ordnet opp i.
Hvis du har et ønske om å teste denne avhengigheten empirisk, finn en variabel motstand, koble i serie en motstand - et amperemeter - en strømkilde (batteri).Det er også ønskelig å sette inn en bryter i kretsen - en vanlig vippebryter.
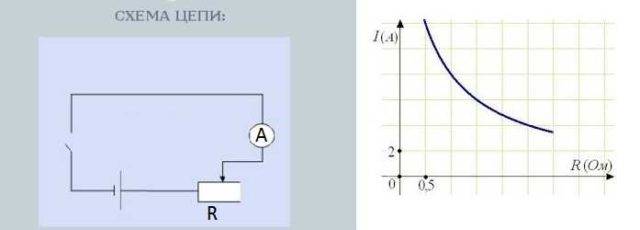
Krets for testing av strømavhengighet av motstand
Ved å vri på motstandsknappen endres motstanden. Samtidig endres også avlesningene på amperemeteret, som måler strømstyrken. Dessuten, jo større motstand, jo mindre avviker pilen - jo mindre strøm. Jo lavere motstand, jo mer avviker pilen - strømmen er større.
Strømmens avhengighet av motstand er nesten lineær, det vil si at den reflekteres på grafen som en nesten rett linje. Hvorfor nesten - dette bør diskuteres separat, men det er en annen historie.
Ohms lov for vekselstrøm
Ved beregning av AC-kretser, i stedet for begrepet motstand, introduseres begrepet "impedans". Impedansen er betegnet med bokstaven Z, den inkluderer den aktive motstanden til lasten Ren og reaktans X (eller Rr). Dette skyldes formen på den sinusformede strømmen (og strømmer av andre former) og parametrene til de induktive elementene, så vel som byttelovene:
- Strømmen i en induktiv krets kan ikke endres umiddelbart.
- Spenningen i en krets med kapasitans kan ikke endres umiddelbart.
Dermed begynner strømmen å ligge etter eller lede spenningen, og den tilsynelatende kraften er delt inn i aktiv og reaktiv.
U=I/Z
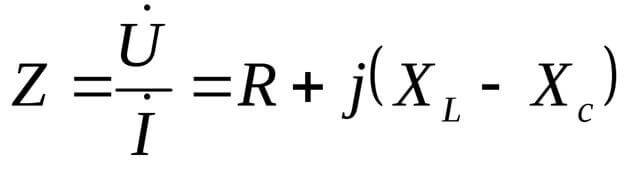
XL og XC er de reaktive komponentene i lasten.
I denne forbindelse introduseres verdien cosФ:
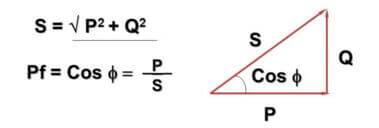
Her - Q - reaktiv effekt på grunn av vekselstrøm og induktiv-kapasitive komponenter, P - aktiv effekt (fordives i aktive komponenter), S - tilsynelatende effekt, cosФ - effektfaktor.
Du har kanskje lagt merke til at formelen og dens representasjon krysser Pythagoras teorem. Dette er sant, og vinkelen Ф avhenger av hvor stor den reaktive komponenten av lasten er - jo større den er, jo større er den.I praksis fører dette til at strømmen som faktisk går i nettet er større enn det en husstandsmåler tar i betraktning, mens bedriftene betaler for full effekt.
I dette tilfellet presenteres motstanden i kompleks form:
Her er j en tenkt enhet, som er typisk for den komplekse formen av ligninger. Mindre ofte referert til som i, men i elektroteknikk er den effektive verdien av vekselstrømmen også betegnet, derfor, for ikke å bli forvirret, er det bedre å bruke j.
Den imaginære enheten er √-1. Det er logisk at det ikke finnes et slikt tall når du kvadrerer, noe som kan resultere i et negativt resultat på "-1".
Når Ohms lov inntreffer
Å skape ideelle forhold er ikke lett. Selv i rene ledere varierer elektrisk motstand med temperaturen. Dens reduksjon minimerer aktiviteten til molekylene i krystallgitteret, noe som forenkler bevegelsen av frie ladninger. Ved et visst nivå av "frysing" oppstår effekten av superledning. Den motsatte effekten (forringelse av ledningsevnen) observeres ved oppvarming.
Samtidig beholder elektrolytter, metaller og visse typer keramikk elektrisk motstand uavhengig av strømtettheten. Stabiliteten til parametrene mens du opprettholder et visst temperaturregime gjør det mulig å bruke formlene til Ohms lov uten ytterligere korreksjoner.
Halvledermaterialer og gasser er preget av varierende elektrisk motstand. Denne parameteren påvirkes betydelig av gjeldende intensitet i kontrollvolumet. For å beregne ytelsesegenskapene må spesialiserte beregningsmetoder brukes.
Dersom vekselstrøm vurderes, korrigeres beregningsmetoden.I dette tilfellet må tilstedeværelsen av reaktive komponenter tas i betraktning. Med motstandens resistive natur er det mulig å anvende de betraktede beregningsteknologiene basert på formlene til Ohms lov.
Kirchhoffs lover.
Fordeling
strømmer i grenene til den elektriske kretsen
adlyder Kirchhoffs første lov,
og fordelingen av spenninger over seksjoner
kjeden adlyder Kirchhoffs andre lov.
Kirchhoffs lover
sammen med Ohms lov er de viktigste
i teorien om elektriske kretser.
Den første
Kirchhoffs lov:
Algebraisk
summen av strømmene i noden er null:
Jeg
= 0 (19)
Hvor
Jeg
er antall grener som konvergerer ved en gitt node.
Det vil si summering
strekker seg til strømmene i grenene,
som konvergerer i det betraktede
node.
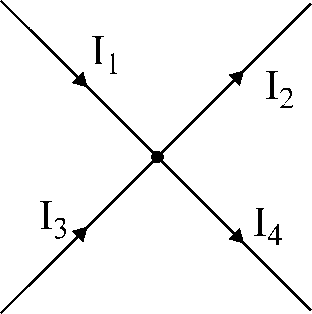
Fig.17. Illustrasjon
til Kirchhoffs første lov.
Antall
ligninger satt sammen i henhold til den første
Kirchhoffs lov bestemmes av formelen:
Nup
= Nu
– 1,
Hvor
Nu
er antall noder i den betraktede kjeden.
Tegn på strømmer i
ligninger tas med i betraktning de valgte
positiv retning. Skilter kl
strømmene er de samme hvis strømmene er de samme
orientert i forhold til dette
node.
For eksempel,
for noden vist i fig. 17:
vi tildeler tegn til strømmene som flyter til noden
"+", og til strømmene som strømmer fra noden - tegn
«-».
Så ligningen
i henhold til Kirchhoffs første lov skal den skrives
Så:
Jeg1
- JEG2
+ jeg3
- JEG4
= 0.
ligninger,
kompilert i henhold til Kirchhoffs første lov,
kalles noder.
Dette
loven uttrykker det faktum at i noden
elektrisk ladning akkumuleres ikke
og blir ikke konsumert. Mengden elektrisk
kostnader som kommer til nettstedet er lik summen
ladninger som forlater noden i ett og samme
samme tidsrom.
Sekund
Kirchhoffs lov:
Algebraisk
sum av emf i enhver lukket krets
kjeden er lik den algebraiske summen av fallet
spenning på elementene i denne kretsen:
Ui
=
Ei
IiRi=Ei(20)
Hvor
Jeg
- elementnummer (motstand eller
spenningskilde) i den betraktede
kontur.
**Antall
ligninger satt sammen i henhold til den andre
Kirchhoffs lov bestemmes av formelen:
Nup
= NB
- Nei
+ 1 – Ned.s.
Hvor
NB
- antall grener av den elektriske kretsen;
Nu
— antall noder;
Ned.s.
er antallet ideelle emk-kilder.
Fig.18. Illustrasjon
til Kirchhoffs andre lov.
Til,
å skrive den andre loven riktig
Kirchhoff for en gitt kontur, følger
overholde følgende regler:
-
vilkårlig
velg retningen til konturomløpet,
for eksempel med klokken (fig. 18). -
emf
og spenningsfall som matcher
i retningen med den valgte retningen
bypass er skrevet i et uttrykk med
tegn "+"; hvis e.f.s. og spenningsfall
samsvarer ikke med retningen
kontur, så innledes de med et tegn
«-».
For eksempel,
for konturen av fig. 18, Kirchhoffs andre lov
vil bli skrevet som følger:
U1
– U2
+ U3
= E1
–E3
–E4
(21)
Ligning (20) kan være
omskriv som:
(Ui
– Ei)
= 0 (22)
Hvor
(U
– E)
- spenning på greinen.
Følgelig
Kirchhoffs andre lov kan formuleres
på følgende måte:
Algebraisk
summen av spenningene på grenene i evt
lukket sløyfe er null.
Potensiell
diagrammet diskutert tidligere tjener
grafisk tolkning av den andre
Kirchhoffs lov.
Oppgave nummer 1.
PÅ
kretsen i fig. 1 er gitt strømmer I1
og jeg3,
motstand og emf Bestem strømmer
Jeg4,
Jeg5,
Jeg6
; spenning mellom punktene a
og b
hvis jeg1
= 10mA,
Jeg3
= -20 mA,
R4
= 5kOhm,
E5
= 20B,
R5
= 3kOhm,
E6
= 40B,
R6
= 2kOhm.
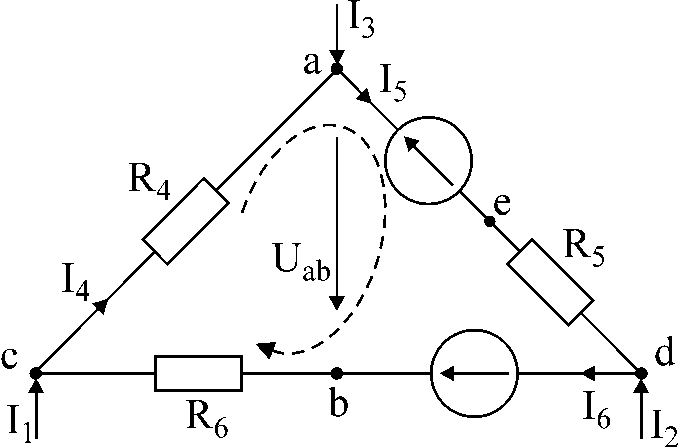
Figur 1
Løsning:
-
For en gitt
kontur, komponerer vi to likninger iht
Kirchhoffs første lov og en - iht
sekund. Konturretning
angitt med en pil.

PÅ
som et resultat av løsningen vi får: I6
= 0; Jeg4
= 10mA;
Jeg5
= -10mA
-
spørre
spenningsretning mellom punktene
en
og b
fra punkt "a"
til punkt "b"
— Uab.
Denne spenningen kan finnes fra ligningen
Kirchhoffs andre lov:
Jeg4R4
+ Uab
+ jeg6R6
= 0
Uab
= - 50V.
Oppgave nummer 2.
Til
diagrammer i fig. 2 tegner likninger iht
Kirchhoffs lover og bestemme de ukjente
poeng.
Gitt:
Jeg1
= 20mA;
Jeg2
= 10mA
R1
= 5kOhm,
R3
= 4kOhm,
R4
= 6kOhm,
R5
= 2kOhm,
R6
= 4kΩ.
Fig.2
Løsning:
Antall noder
ligninger - 3, antall konturligninger
– 1.
Huske!
Når du kompilerer ligningen i henhold til den andre
Kirchhoffs lov velger vi konturen, i
som ikke inkluderer aktuelle kilder.
Konturens retning er angitt i figuren.
PÅ
av denne kretsen, strømmene til grenene I1
og jeg2.
Ukjent
strømmer
Jeg3,
Jeg4,
Jeg5,
Jeg6.

Bestemmer seg
system, får vi: I3
= 13,75 mA;
Jeg4
= -3,75mA;
Jeg5
= 6,25mA;
Jeg6
= 16,25mA.
Enkle konsepter
Elektrisk strøm flyter når en lukket krets lar elektroner bevege seg fra et høyt potensial til et lavere i kretsen. Med andre ord krever strømmen en elektronkilde som har energien til å sette dem i bevegelse, samt et punkt for deres retur av negative ladninger, som er preget av deres mangel. Som et fysisk fenomen er strømmen i en krets preget av tre grunnleggende størrelser:
- Spenning;
- gjeldende styrke;
- motstanden til en leder som elektroner beveger seg gjennom.
Styrke og spenning
Strømstyrken (I, målt i ampere) er volumet av elektroner (ladning) som beveger seg gjennom et sted i kretsen per tidsenhet.Med andre ord, måling I er bestemmelsen av antall elektroner i bevegelse
Det er viktig å forstå at begrepet kun refererer til bevegelse: statiske ladninger, for eksempel på polene til et ikke-tilkoblet batteri, har ikke en målbar verdi på I. Strøm som flyter i én retning kalles direkte (DC), og periodisk skiftende retning kalles alternerende (AC). Spenning kan illustreres ved et slikt fenomen som trykk, eller som forskjellen i den potensielle energien til objekter under påvirkning av tyngdekraften
For å skape denne ubalansen, må du først bruke energi, som vil bli realisert i bevegelse under passende omstendigheter. For eksempel, i fallet av en last fra en høyde, arbeides det for å løfte den, i galvaniske batterier dannes potensialforskjellen ved terminalene på grunn av konvertering av kjemisk energi, i generatorer - som et resultat av eksponering for et elektromagnetisk felt
Stress kan illustreres ved et slikt fenomen som trykk, eller som forskjellen i den potensielle energien til objekter under påvirkning av tyngdekraften. For å skape denne ubalansen, må du først bruke energi, som vil bli realisert i bevegelse under passende omstendigheter. For eksempel, i fallet av en last fra en høyde, blir arbeidet med å løfte det realisert, i galvaniske batterier dannes potensialforskjellen ved terminalene på grunn av konvertering av kjemisk energi, i generatorer - som et resultat av eksponering for en elektromagnetisk felt.
Ledermotstand
Uansett hvor god en vanlig leder er, vil den aldri tillate elektroner å passere uten en viss motstand mot deres bevegelse.Det er mulig å betrakte motstand som en analog av mekanisk friksjon, selv om denne sammenligningen ikke vil være perfekt. Når det går strøm gjennom en leder, blir en viss potensialforskjell omdannet til varme, så det vil alltid være et spenningsfall over motstanden. Elektriske varmeovner, hårfønere og andre lignende enheter er designet utelukkende for å spre elektrisk energi i form av varme.
Forenklet motstand (betegnet som R) er et mål på hvor mye strømmen av elektroner er forsinket i en krets. Det måles i ohm. Konduktiviteten til en motstand eller et annet element bestemmes av to egenskaper:
- geometri;
- materiale.
Form er av største betydning, som det fremgår av den hydrauliske analogien: å skyve vann gjennom et langt og smalt rør er mye vanskeligere enn å skyve vann gjennom et kort og bredt. Materialer spiller en avgjørende rolle. For eksempel kan elektroner bevege seg fritt i en kobbertråd, men kan ikke strømme i det hele tatt gjennom isolatorer som gummi, uansett form. I tillegg til geometri og materiale er det andre faktorer som påvirker ledningsevnen.
Ohms lovtolkning
For å sikre bevegelse av ladninger, må du lukke kretsen. I fravær av ekstra kraft kan ikke strømmen eksistere i lang tid. Potensialene vil raskt bli like. For å opprettholde driftsmodusen til kretsen, er det nødvendig med en ekstra kilde (generator, batteri).
Den komplette kretsen vil inneholde den totale elektriske motstanden til alle komponentene. For nøyaktige beregninger tas tap i ledere, resistive elementer og en strømkilde i betraktning.
Hvor mye spenning som må brukes for en viss strømstyrke, beregnes ved hjelp av formelen:
U=I*R.
På samme måte, ved hjelp av de betraktede relasjonene, bestemmes andre parametere i kretsen.
Parallell og seriell tilkobling
I elektro, er elementer koblet enten i serie - etter hverandre, eller parallelt - dette er når flere innganger er koblet til ett punkt, og utganger fra de samme elementene kobles til et annet.
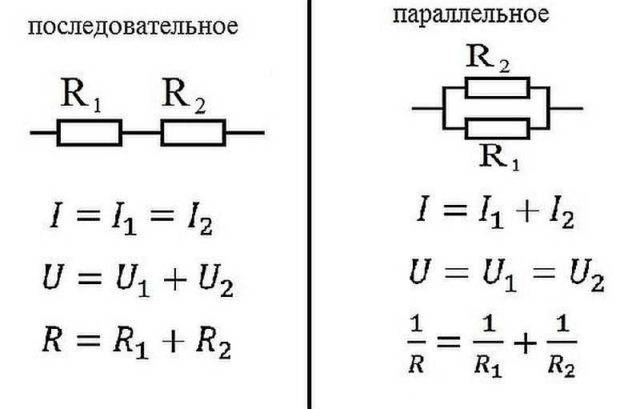
Ohms lov for parallell- og seriekobling
seriell tilkobling
Hvordan fungerer Ohms lov for disse sakene? Når koblet i serie, vil strømmen som flyter gjennom kjeden av elementer være den samme. Spenningen til en seksjon av en krets med elementer koblet i serie beregnes som summen av spenningene i hver seksjon. Hvordan kan dette forklares? Strømstrømmen gjennom et element er overføringen av en del av ladningen fra en del av den til en annen. Jeg mener, det er litt arbeid. Størrelsen på dette arbeidet er spenning. Dette er den fysiske betydningen av stress. Hvis dette er klart, går vi videre.
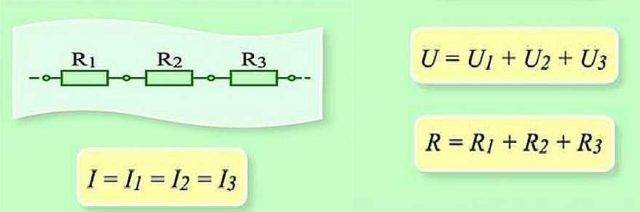
Seriell tilkobling og parametere for denne delen av kretsen
Ved seriekopling er det nødvendig å overføre ladningen etter tur gjennom hvert element. Og på hvert element er dette et visst "volum" av arbeid. Og for å finne mengden arbeid på hele delen av kjeden, må du legge til arbeidet på hvert element. Så det viser seg at den totale spenningen er summen av spenningene på hvert av elementene.
På samme måte - ved hjelp av addisjon - finner man også den totale motstanden til kretsseksjonen. Hvordan kan du forestille deg det? Strømmen som flyter gjennom kjeden av elementer overvinner sekvensielt alle motstander. En etter en. Det vil si at for å finne motstanden som han overvant, er det nødvendig å legge sammen motstandene. Mer eller mindre slik.Den matematiske utledningen er mer komplisert, og det er lettere å forstå mekanismen til denne loven.
Parallellkobling
En parallellforbindelse er når begynnelsen av lederne / elementene konvergerer på ett punkt, og i et annet er endene deres koblet sammen. Vi vil prøve å forklare lovene som er gyldige for forbindelser av denne typen. La oss starte med strøm. En strøm av en viss størrelse tilføres til koblingspunktet til elementene. Den skiller seg, flyter gjennom alle lederne. Fra dette konkluderer vi med at den totale strømmen i seksjonen er lik summen av strømmen i hvert av elementene: I = I1 + I2 + I3.
Nå for spenningen. Hvis spenning er arbeid for å flytte en ladning, vil arbeidet som er nødvendig for å flytte en ladning være det samme på ethvert element. Det vil si at spenningen på hvert parallellkoblede element vil være den samme. U=U1=U2=U3. Ikke så morsomt og visuelt som i tilfellet med forklaringen av Ohms lov for en kjedeseksjon, men du kan forstå.
Lover for parallellkobling
For motstand er ting litt mer komplisert. La oss introdusere konseptet konduktivitet. Dette er en egenskap som indikerer hvor lett eller vanskelig det er for en ladning å passere gjennom denne lederen. Det er klart at jo lavere motstand, jo lettere vil det være for strømmen å passere. Derfor beregnes konduktivitet - G - som resiprok av motstand. I formelen ser det slik ut: G = 1/R.
Hvorfor snakker vi om konduktivitet? Fordi den totale ledningsevnen til en seksjon med parallellkobling av elementer er lik summen av ledningsevnen for hver av seksjonene. G = G1 + G2 + G3 - lett å forstå. Hvor lett strømmen vil overvinne denne noden av parallelle elementer, avhenger av ledningsevnen til hvert av elementene. Så det viser seg at de må brettes.
Nå kan vi gå videre til motstand.Siden konduktivitet er resiprok av motstand, kan vi få følgende formel: 1/R = 1/R1 + 1/R2 + 1/R3.
Hva gir oss en parallell og seriell forbindelse?
Teoretisk kunnskap er bra, men hvordan bruke det i praksis? Elementer av enhver type kan kobles parallelt og i serie. Men vi vurderte bare de enkleste formlene som beskriver lineære elementer. Lineære elementer er motstander, som også kalles "motstander". Så her er hvordan du kan bruke det du har lært:
Hvis det ikke er en høyverdig motstand tilgjengelig, men det finnes flere mindre, kan ønsket motstand oppnås ved å koble flere motstander i serie. Som du kan se, er dette en nyttig teknikk.
For å forlenge levetiden til batteriene kan de kobles parallelt. Spenningen i dette tilfellet, i henhold til Ohms lov, vil forbli den samme (du kan være sikker ved å måle spenningen med et multimeter). Og "levetiden" til et dobbelt batteri vil være mye lengre enn for to elementer som vil erstatte hverandre
Bare merk: kun strømforsyninger med samme potensial kan kobles parallelt. Det vil si at et dødt og et nytt batteri ikke kan kobles til.
Hvis du fortsatt kobler til, vil batteriet som har en større ladning ha en tendens til å lade et mindre ladet. Som et resultat vil deres totale ladning falle til en lav verdi.
Generelt er dette de vanligste bruksområdene for disse forbindelsene.
Ideell EMF-kilde
Elektromotorisk kraft (E) er en fysisk størrelse som bestemmer graden av påvirkning av ytre krefter på bevegelsen i en lukket krets av ladningsbærere. Med andre ord, hvor sterkt strømmen har en tendens til å flyte gjennom lederen vil avhenge av EMF.
Når man forklarer slike uforståelige fenomener, liker innenlandske skolelærere å vende seg til metoden for hydrauliske analogier. Hvis en leder er et rør, og elektrisk strøm er mengden vann som strømmer gjennom den, så er EMF trykket som en pumpe utvikler for å pumpe væske.
Begrepet elektromotorisk kraft er relatert til et slikt konsept som spenning. Hun, EMF, måles også i volt (enhet - "V"). Hver strømkilde, det være seg et batteri, en generator eller et solcellepanel, har sin egen elektromotoriske kraft. Ofte er denne EMF nær utgangsspenningen (U), men alltid litt mindre enn den. Dette er forårsaket av den indre motstanden til kilden, hvor en del av spenningen uunngåelig faller.
Av denne grunn er den ideelle kilden til EMF snarere et abstrakt konsept eller en fysisk modell som ikke har noen plass i den virkelige verden, fordi den interne motstanden til batteriet Rin, selv om den er veldig lav, fortsatt er forskjellig fra absolutt null.
Ideell og reell kilde til emf
I differensiell form
Formelen presenteres veldig ofte i en differensiell form, siden lederen vanligvis er inhomogen og det vil være nødvendig å dele den opp i de minste mulige seksjonene. Strømmen som går gjennom den er assosiert med størrelse og retning, så den regnes som en skalar mengde. Når den resulterende strømmen gjennom en ledning skal finnes, tas den algebraiske summen av alle de individuelle strømmene. Siden denne regelen kun gjelder for skalarmengder, tas strømmen også som en skalarmengde. Det er kjent at strømmen dI = jdS går gjennom seksjonen. Spenningen på den er Edl, så for en ledning med konstant tverrsnitt og lik lengde vil forholdet være sant:
 Differensiell form
Differensiell form
Derfor vil uttrykket av strømmen i vektorform være: j = E.
Viktig! Ved metalliske ledere avtar konduktiviteten med økende temperatur, mens den for halvledere øker. Omovs lov viser ikke streng proporsjonalitet
Motstanden til en stor gruppe metaller og legeringer forsvinner ved en temperatur nær absolutt null, og prosessen kalles superledning.